NSGA-II提出原文 A fast and elitist multiobjective genetic algorithm: NSGA-II

即带有精英保留策略的快速非支配多目标优化算法，是一种基于Pareto最优解的多目标优化算法。

Pareto（柏拉图）支配

MOP问题中支配是一个重要的概念

MOP多目标优化问题

支配的描述为：有两个解x1和x2，x1支配x2的充要条件是对于任意的i(i=1,2, 3…m)，均有fi(x1)<=fi(x2)，且对于任意的i(i=1, 2, 3…m)，存在fi(x1)<fi(x2)。记为x1≺x2。（和离散数学里的偏序关系相似）

Pareto最优解（Pareto Optimal Solution）

某个解x’是最优解，当且仅当x’不被任何其他解支配。 x’只是不被其他解支配，而不是支配了其他所有解，就能称为最优解了。

Pareto集（Pareto Set）

如果一组解集（也就是多个x）中的任意两个解都不能支配对方，那么这个集合称为Pareto集，简称PS

Pareto前沿（Pareto Front）

PS中，每个解对应的目标函数值组成的集合称为pareto前沿，简称PF。

进化算法是如何解决MOP问题的呢？

主要是3个应用：变异、交叉、多样性。

1.变异（类似生物变异，优胜劣汰）

1. 取某一个解x0，让x0随机地变化，比如增加0.1得x1，减少0.1得x2之类，看看变化之后和原来有什么不同。 要是变化之后，发现了更左下的点？就说明发现了更优的解，这时可以保留左下的点、淘汰右上的点。 需要注意的是：变异不是一定能够产生更左下的点的，但是只要出现了，我们就能把它保留下来！

2.交叉

叫做交配更好理解。假如有两个解x1和x2，分别对应左上的p1和右下的p2，那么我们可以想办法融合x1和x2的优良性状，这就是交叉。 比如，我们可以取x3=(x1+x2)/2，看看x3相对于x1和x2的位置，要是x3是更优的解，同样可以保留x3。 和变异相同，交叉也不是一定能产生更左下的点的。

3.多样性

多样性就是：保持找到尽可能多的解的可能性。

NSGA：进化思想

NSGA-Ⅱ中还包含了一个选择个体的方法：拥挤度比较

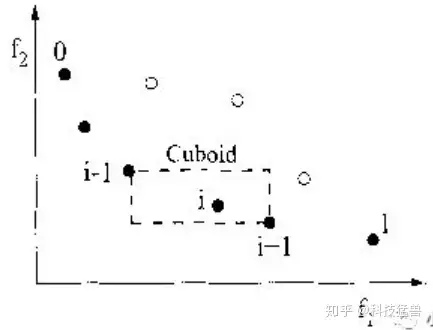
i的拥挤度和i-1点和i+1点的位置有关，上图i点的拥挤度就是方形的周长（也就是虚线的总长度）。最左边和最右边的点的拥挤度设置为无限大。

我们喜欢拥挤度大的点（拥挤度大实际上是和周围的点相隔远），因为它们更能保持种群多样性，更容易发展出新种群。

左上和右下的点是无法比较的，但是拥挤度提供了一个比较的思路。

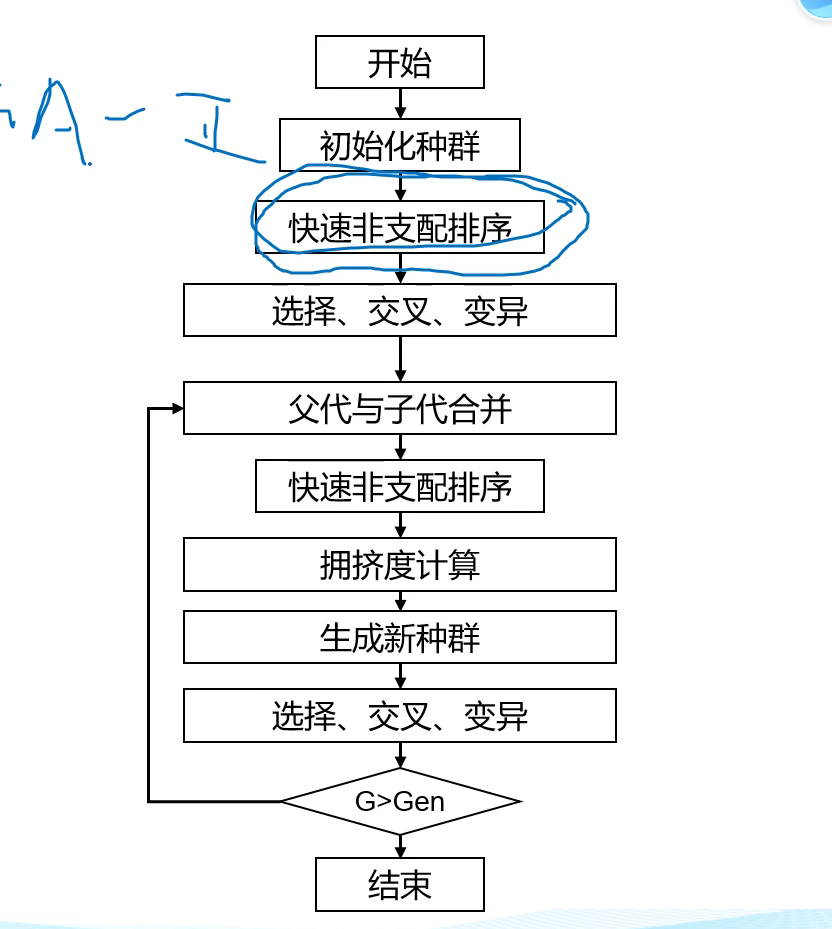
NSGA流程

1.初始化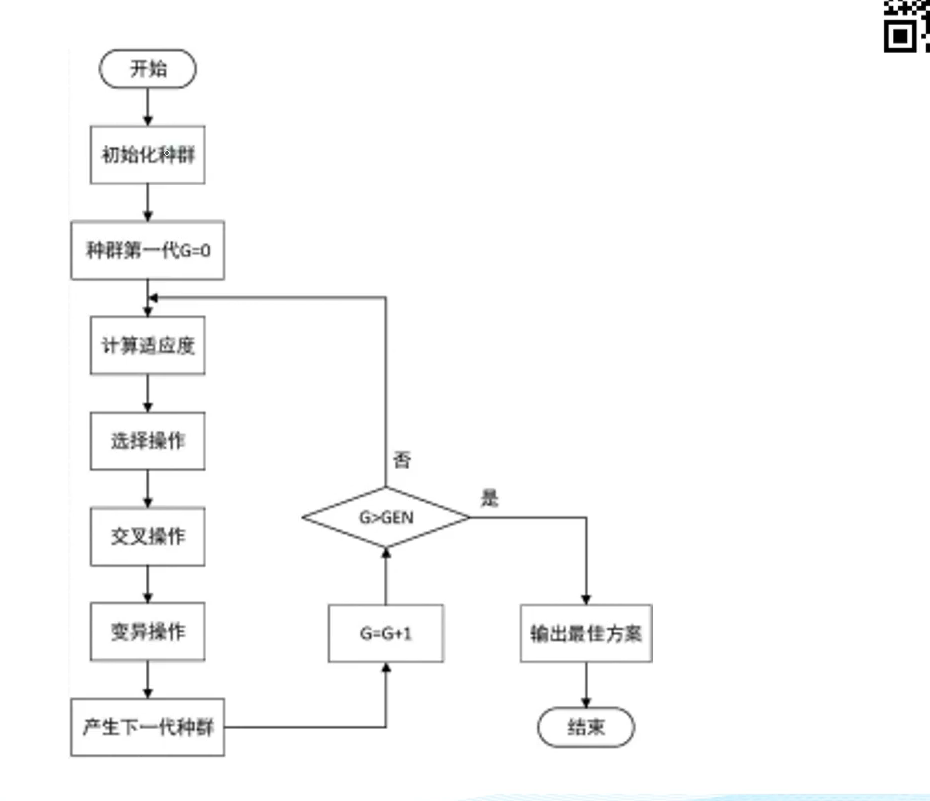

2.交叉变异

3.非支配排序

Pareto等级：在一组解中，非支配解Pareto等级定义为1，将非支配解从解的集合中删除，剩下解的Pareto等级定义为2，依次类推，可以得到该解集合中所有解的Pareto等级。

把种群分成几个PS并赋予等级，越往左下的PS等级越高（因为越优）。rank越小，等级越高

3.1选择

选择等级高的个体，rank=1和rank=2的个体，总共3个被保留

迭代 选择完了又回到第2步，直到进化到了一定的次数，结束算法